Archive - 2017
Tuesday, November 21, 2017
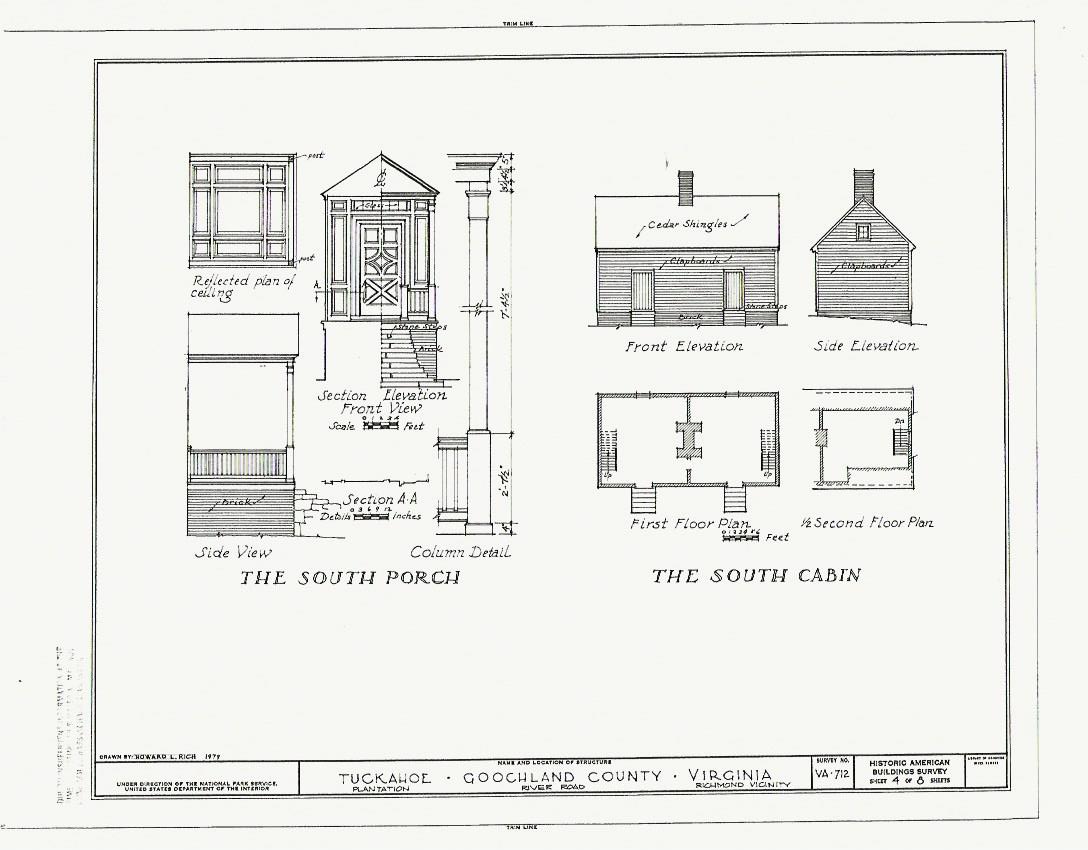
The Tuckahoe Cabin Geometry
This is the double slave cabin at Tuckahoe Plantation, Thomas Jefferson's childhood home in Virginia.
I have written about it before:
http://www.jgrarchitect.com/2014/06/cabin-tuckahoe-plantation-goochland.html
The simplicity of the cabin and its HABS drawing make it an easy building to use when I teach hands-on Practical Geometry.
The beautiful hand drawn lines and details of HABS drawings fascinate students. And they get a little history.
Here the elaborate paneled front door for the plantation house, its ceiling pattern, and columns are shown with the little, uncomplicated cabin.
Craft, wealth, slavery c, 1750, are visible side by side.
Remember that you can click the drawings to enlarge them.
The cabin illustrates the Rule of Thirds.
Students unused to geometry can grasp the basics quickly as they discover the design simplicity of the floor plan.They explore the geometry of the elevations with curiosity, not in trepidation.
For a tutorial on the Rule of Thirds:
http://www.jgrarchitect.com/2016/10/practical-geometry-drawing-diagrams.html
BUT - This is academic.
How did a carpenter actually use this knowledge?
I wasn't there. So, I am guessing? No.
I've read the written documents, 'read' the drawings that have no words - from that period and the more recent era of HABS. I've measured and documented these buildings, participated in repairing and framing them as well as their deconstruction.
I make connections to the old ways of laying out a frame from the way we lay out today using the same tools our ancestors had - a line, a square, a plumb bob, a pencil - and a compass.
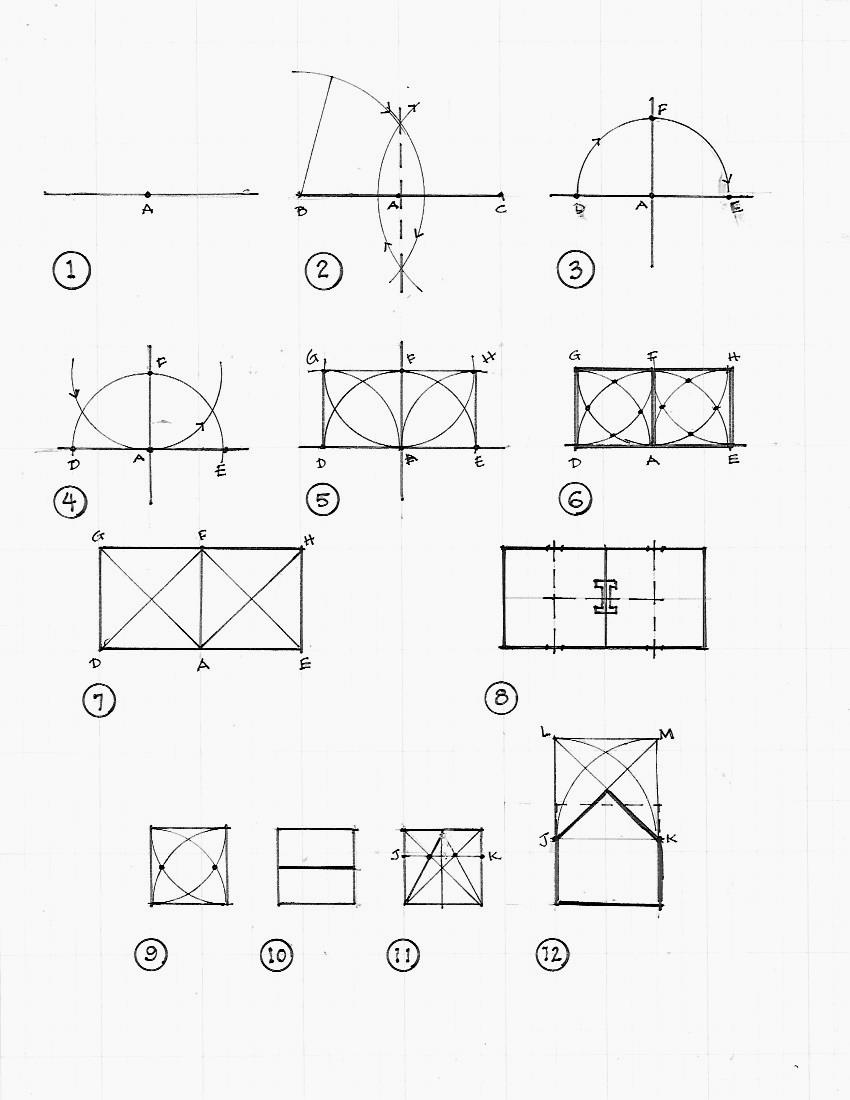
Here is a construction scenario for this cabin.
The carpenter plans to build a 2 room cabin with a loft, 2 doors, 2 windows, back to back fireplaces on this site.
The size is standard, each room about 16' x 16'. He either builds right here, or he uses a framing floor. In either case it is a flat, level surface. His geometry will establish his points and keep his frame square.
He measures off 16' with twine, using his own handmade rule. He then stretches out his twine another 16-20 ft, pulls it taut.
He now has a straight Line.
Maybe he has chalk and snaps it, making a line. Maybe he pegs it.
Modern carpenters snap and set lines regularly. We still call them 'lines'.
1 - On his Line he marks his first point (A).
2 - He chooses a radius and draws 2 arcs, one with its center at (B), one with its center at (C). He now has 2 points where his arcs cross and can draw a line perpendicular to his Line.
3 - He chooses his dimension - here, 16 ft - puts his compass - perhaps a string with a knot at 16' - at (A) and draws a semi-circle (D-E).
Now he has a new point (F). His cabin is now 32' long; its width is 16' (A-F)
4 - Using (F) as his center he draws another semi-circle.
5 - Then he draws 2 quarter circles using (D) and (E) as his centers. Where the arcs cross (G) and (H) are the upper corners of his cabin.
6 - He swings the other arcs, and now has 4 internal points in each room of the cabin. He marks those points.
7 - Just to be sure, he trues up the space by checking that his diagonals are equal (G-A, D-F etc.).
8 - The interior points give him the centers for the doors, windows, and fireplaces. The plan of the cabin is done.
The end elevation, or the 3 bents of the frame:
9 - He sets up the 16' square with its arcs.
10 - The interior points give him the location for the 2nd floor joists.
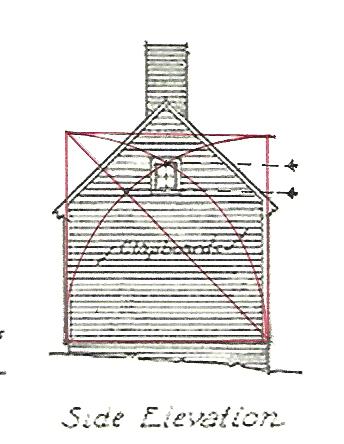
11 - The points also give him the center of his elevation. He can draw his Lines and use the Rule of Thirds to find the upper third of his square (J-K).
12 - (J) and (K) mark the eaves for the roof. He extends the sides of the square, draws his arcs to find the upper corners ( L) and (M), adds his diagonals (J-M) and (L-K). Ahh - there's the roof!
The window in the eaves is placed and sized:
A carpenter before the Industrial Revolution would not need my description. He would have learned the geometry as an apprentice. If he needed a reminder he would practice a bit with his compass. He probably didn't have a drawing for such a simple cabin.
However, books with instructions to builders (not architects) did exist. Here are 2 examples.
Batty Langley in The Builder's Director, London, 1751, draws moldings "Proportioned by Minutes and by Equal Parts". He writes that his little book is to be available to "Workmen" and "any common Laborer."
These window and door 'Weatherings' are all composed of squares and arcs of circles. Langely lays out the parts; the Workman can read the rest.
Asher Benjamin in The Country Builder's Assistant, Greenfield, MA, 1797, says his book "will be particularly useful to Country Workmen in general".
He assumes the Workman knows geometry.
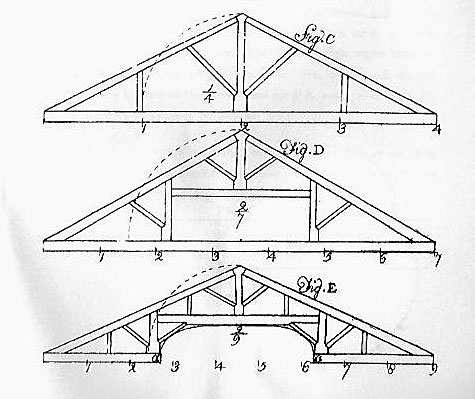
Plate XXIX says only
"C, is a roof; divide the width of the building into 4 parts, one of which will be the perpendicular height. Divide Fig. D, into 7 parts,give 2 to the perpendicular height.
Fig. E, is intended for a roof to a Meetinghouse; divide the width of the building into 9 parts; give 2 to the perpendicular height; the ends of the Beams, a, a, are to be supported by columns."
My first post on Tuckahoe Plantation is here:
https://www.jgrarchitect.com/2014/06/cabin-tuckahoe-plantation-goochland.html